Before you start

Drawing lines and curves on paper is a skill most people have been practicing since kindergarten. In FreeSewing, we draw lines and curves with code, which is a bit more abstract but doesn't have to be complicated once you understand a few basic building blocks.

Understanding the concepts that are involved in designing sewing patterns in code will pay dividends later. That is why we recommend you familiarize yourself with the following topics:

note

There's no need to know everything

FreeSewing sits at the intersection of the world of makers and developers. If your background is in development, you will need no explaining what SVG is but might not know much about designing sewing patterns. If on the other hand your background is in sewing or pattern design, you might wonder what the heck NodeJS is and why you should care.

Few people straddle both worlds, so as you start using FreeSewing, chances are you'll learn a few new things along the way.

And if you get stuck our chatrooms on Discord are the best place to get help.

Scalable Vector Graphics

Patterns are rendered as SVG — short for Scalable Vector Graphics — an XML-based vector image format and an open standard. While you don’t need to be an SVG expert, a basic understanding of the format will greatly help you to understand FreeSewing.

For example, the coordinate system and the way paths are structured are all related to the SVG drawing system, which is closely related to other 2D drawing technologies such as PostScript or PDF.

The coordinate system

The coordinate system in FreeSewing -- and in SVG -- follows the same rules as text on a page. You start at the top-left, and as you go to the right, the X-coordinate will increase. As you go down the Y-coordinate will increase.

Preview

Code

({ Point, points, paths, Path, part }) => {
  points.origin = new Point(10, 10)
  points.x = new Point(100, 10)
  points.y = new Point(10, 50)
  points.textX = new Point(85, 20).addText('X', 'text-lg')
  points.textY = new Point(12, 43).addText('Y', 'text-lg')
  paths.coords = new Path()
    .move(points.y)
    .line(points.origin)
    .line(points.x)
    .addClass('mark')
    .attr('marker-start', 'url(#dimensionFrom)')
    .attr('marker-end', 'url(#dimensionTo)')

  return part
}

X-Ray

The coordinate system in an SVG document

The image above illustrates both the X-axis and Y-axis. On the X-axis, 20 is further to the right than 10. On the Y-axis, 50 is lower than 20.

note

The Y-axis is inverted in many drawing programs, with the origin (0,0) being the lower left corner, rather than the upper left corner.

This is a common point of confusion so keep in mind that the Y-axis may not behave as you would have intuitively expected.

Units in FreeSewing

FreeSewing uses millimeter (mm) for all its internal units. We do support both imperial and metrics units, which are displayed as cm or inch, but under the hood everything is handled in millimeter.

So as a pattern designer, you will work with mm. When you write 1, that’s one millimeter. When you write 7.8, that’s 7.8 mm.

While you can use cm or inch on the FreeSewing website, that is merely a layer of abstraction on top of the internal units, which are always mm.

Understanding Bézier curves

While lines on computers are easy to store with a start and end point, curves require more information. In FreeSewing — as in SVG and countless of other computer applications — curves are stored as Bézier curves, named after French engineer Pierre Bézier who popularized their use back in the 1960s.

In FreeSewing, we use so-called cubic Bézier curves which have:

• A start point
• A first control point that’s linked to the start point
• A second control point that’s linked to the end point
• An end point

Preview

Code

({ Point, points, Path, paths, part }) => {

  points.from = new Point(10, 20)
  points.cp1 = new Point(40, 0)
  points.cp2 = new Point(60, 40)
  points.to = new Point(90, 20)

  paths.line = new Path()
    .move(points.from)
    .curve(points.cp1, points.cp2, points.to)
    .setText("Path.curve()", "text-sm center fill-note")

  return part
}

X-Ray

An example of a Bézier curve drawn by the Path.curve() method

Bézier curves and their handles or control points are surprisingly intuitive. The following illustration does a great job at explaining how they are constructed:

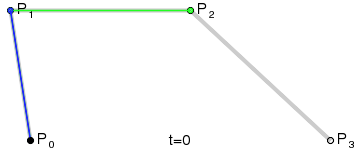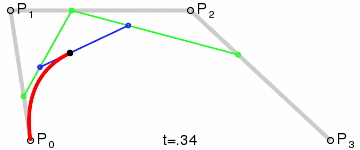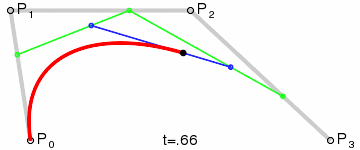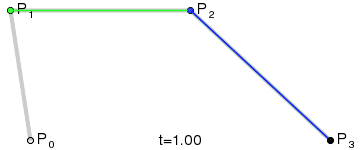
You don't need to understand the mathematics behind Bézier Curves. As long as you intuitively get how the control points influence the curve, you're good to go.

note

More on Bézier curves

Wikipedia has a good introduction to Bézier curves. For a deep-dive into the subject, check out A Primer on Bézier Curves by Pomax.